こ
の
先
ネ
タ
バ
レ
Ｏ
Ｋ
？

★算数
[1]　小問集合
　小問集合の占めるスペースが年々大きくなってるような…今年はなんと2枚目の右上まで進攻してきてる。
(1)計算の工夫　(2)計算　(3)逆算　(4)計算
　難しい計算はなく、当然間違えられないものばかり。
　(1)は明らかに分配法則を意図した形であるものの、それを実行しても数字が全然奇麗にならないというのがちょっと謎。
(5)面積
　対角線の補助線を引いて2つの三角形に分ける超有名題。
(6)濃度算
　食塩水の混合だが、面積図を使うまでもない、ただの計算問題。
(7)規則性or植木算
　正六角形を並べたときのまわりの長さについての問題。
　1枚ずつ増やしたときの規則を考えるか、全体から重なりを引くか。
　易しめの問題が多い1枚目のいいアクセント？になっている。
(8)旅人算
　時間差で出発する兄弟の追いつきについての問題。
　分速が変な値だが答えは普通の値になるので、気にせず計算するべし。
(9)角度
　一組の三角定規を重ねたときの角度。これは死んでも正解せよ。
(10)消去算
　ただ消しゴムの数を揃えればいいだけの超基本題。
(11)数の性質
　5で割ると3余り、7で割ると5余る整数についての問題。
　2を足せば35の倍数になる定番系だがミスしやすい…33の倍数と勘違いしないように！
(12)売買算
　定価通りと値引きで売ったのをあわせて想定の利益を得るようにする。
　難しくはないのだが、小問集合にしては設定が入り組んでいる。
(13)規則性
　0,3,8,15,24,…の数列で13番目を求める。
　高々13番目なので差を取ってひたすら書き出しても答えを出せるが、よく見ると超有名数列の変形版。
(14)やりとり算
　線分図を書いてやりとりを表すタイプの標準レベル。
(15)仕事算
　ポンプAとBを使って水槽を満水にするのにかかる時間を考察する。
　AやBを1台使ったときに満水となる時間は直接与えられてないので、小問集合としてはやや難しい。

[2]図形の移動(平行移動)
　正方形を移動させたときに長方形との重なりの面積を考える。
　土佐塾中の前期入試の大問としては珍しく、枝問のない構成である。
　条件を満たす2通りの状況を作図するのが第一歩だが、そこから正解を出すまでの手数は多く、正解率は低そう。
　なぜ長方形の横を求めさせる前に、正方形の秒速を求めるなどの誘導をつけなかったんだろう？スペースの都合かな？？

[3]立体図形
　立方体を積み上げて作った立体の表面にペンキを塗る問題。
　それだけならとってもありふれた設定だが、(2)では条件に従って1個取り除く方法を問われている。
　土佐塾中の平均層なら、(2)は捨てるのが得策だろう。この大問においては(1)の正解に全力を注ぐべき。

[4]旅人算(ダイヤグラム)
　途中で10分間休憩する2人が出会うのはいつなのかを求める。
　Bのダイヤグラムをある程度正確に書けば、「休憩時間が2人とも同じ」という特殊設定を生かすか、出発してから1時間後の状況から遡っていけばＯＫ。
　見た目ほどは難しくなく、最終問としては易しい。

今年の算数は、大問が[4](1)(2)を除いてどれも骨があるため、大問の(1)で点をもぎ取る戦略が取りにくい。よって、[1]の小問集合でどれだけ稼げたかが勝負どころになりそう。
制限時間は70分と長めではあるものの、1問に時間を食われてたらあっという間に終了時間が来てしまう。

★理科
[1]食物の消化
　前半はだ液の消化実験の考察、後半は養分の消化吸収の知識問題。
　前半は、だ液アミラーゼはヒトの体温付近でないと働かないことだけでなく、温度変化させて働きが再生するかどうかも考えさせるため、平均受験層にはやや解きにくいかもしれない。
　後半は比較的素直な問題なので、正解を重ねたい。

[2]太陽と月の動き
　太陽と月の位置関係から、季節や月の形を考える問題。
　標準レベルではあるものの、月の問題は一般的に差がつきやすいので、きちんと練習しておくこと。

[3]天気の変化
　ひまわりの雲画像から、日本列島の天気がどうなのかを答えさせる。
　雲画像が4つも用意されており、雲の様子をきっちりと読み取らなければならない。
　つまり、「春～周期的な天気変化」「梅雨～日本を東西に覆う帯状の雲」「真夏～日本晴れ」「台風～渦を巻く雲の塊」「真冬～北西の季節風による筋状の雲」のいずれであるのかを判断する。
　学習量がそのまま点に反映される、ほどよい難易度の出題である。

[4]固体の分類
　固体に様々な実験をすることにより、固体の正体を特定する問題。
　5種類の固体のうち、与えられた候補は7つもあり、おこなう実験は6つもあるので、考察はなかなか大変である。
　(4)では5種類の固体を答えさせるため、ここを全問正解すれば大きい。

[5]つりあい総合
　ばねや棒や滑車を使った、様々なつりあいの計算問題。
　(1)ばね単独の問題は解けたとして、それ以降に登場する棒は太さが一様ではない、しかも棒の端をばねで引き上げるという複雑設定のため、土佐塾中の平均受験層には辛い問題だったろう。
　しかもそれに追い討ちをかけるように、最後は滑車が登場…。ただし(6)はちょっと変わった問題なので、土佐上位合格や愛光受験を目指している人には、是非挑戦してもらいたい。

今年の理科はぱっと見て、点が稼げそうな易しい大問はないので、平均点はあまり高くはなさそうである。


★この一題
[3]
1辺の長さが1cmの立方体を、3段とも上から見て正方形になるように、水平な台の上にすき間なく積み重ねて、下の図のような立体をつくり、その表面にペンキをぬりました。ただし、立体が台に触れている面もペンキをぬるものとします。このとき、次の問いに答えなさい。

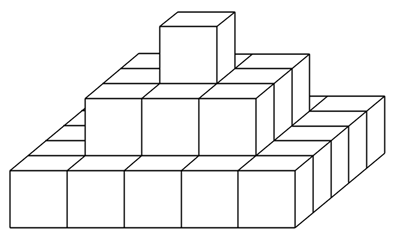
(1)ペンキをぬった表面の面積は何cm²ですか。
(2)この立体からペンキをぬってある立方体を1個だけ取り除いてできた立体の表面を、別の色のペンキでぬり直しました。このとき、別の色でぬった表面の面積が(1)の面積と同じになるように取り除くことができる立方体は何個ありますか。ただし、立方体を取りのぞいたときに残った立方体の位置は変わらないものとします。
→解説だよ