軌跡の問題を考えるときは、次の2つの動きが基本となる。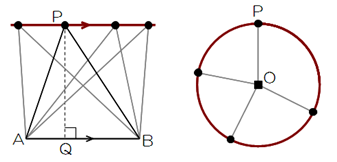
パターン1)△ABPの高さPQが2cmとなるような点Pの軌跡
→辺ABと平行で、その距離が2cmとなる直線となる。
パターン2)点Oは動かず、OPの長さが2cmとなるような点Pの軌跡
→Oを中心とした、半径2cmの円の円周となる。
今回の場合、Pから辺ABに下ろした垂線PQの長さが(2×□÷2=4より)2cmとなる点Pの軌跡を求めるわけだが、立体で考えることに注意しなければならない。
まずは、立方体の表面で考えてみよう。
点Pは辺DC上と辺EF上を動ける(図1)
→これは、パターン1からすぐにわかるだろう。
面EADHや面FBCGでは、点Pは半径2cmの四分円弧を描く(図2)
→点Qが点AやBにあると考えれば、パターン2の動きである。
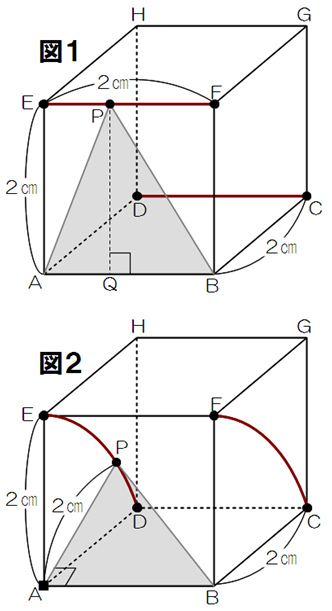
それでは、立方体内部の軌跡はどうなるだろうか。
辺DCを動かして辺EFに重ねるには、面EADHや面FBCGにおける軌跡を参考にする。
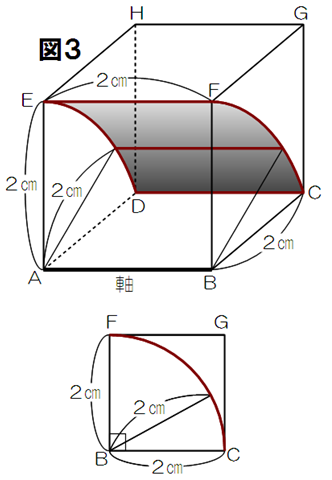
今回の軌跡は辺ABを軸として辺DCを上側に90度回転させたものである。
(四分円弧FCを右から左に2cm平行移動させたもの、と考えてもよい)
Pの動ける範囲は、底面が半径2cmの円柱の側面の一部である。
これは、横が2cm、縦が四分円弧FC→4π÷4=1πcmの長方形と考えることができる。
したがって面積は、2×1π=2π=2×3.14=6.28cm2。
※※※
ゆとり教育脱却の影響なのか、今年の高知県の入試では、本来範囲外とされる出題が算数で見られた。
学芸中では相似、土佐中では柱体。
(範囲外としては他に学芸で場合の数が出題されているが、学芸は以前から一貫して場合の数を出題し続けている)
今後は、範囲外とされていたものも積極的に学習した方がいいだろう。
※※※
参考までに、この問題の応用版と言える問題を掲載しておく。
・[参考問題]H16 灘中 第2日[5](2) ※(1)略、図略、文章改
台形ABCDを底面とする高さ30cmの四角柱がある。
底面ABCDにおいて、角A=角B=90度、AB=64cm、BC=95cm、CD=80cm、DA=143cmである。
点Pがこの立体の内部と表面上を、三角形PCDの面積が2400cm2となるように動くとき、点Pが動ける部分の面積を求めよ。円周率が必要ならば3.14として計算せよ。
↓見たい場合はクリック3連打してみてね
答…2512cm2
PR

