こ
の
先
ネ
タ
バ
レ
O
K
?
★算数第1日
[1]逆算
整数と分数を別個に計算するという基本事項さえわかっていれば簡単。
というか、灘中受験者はこの程度のことで悩むはずがない。
そういえば、最近の計算問題はあまり西暦にこだわってないんやね。
[2]旅人算
2人が周回道路をまわるときのすれ違いと追い越しの問題。
Aが4周したときBはちょうど3周したことから速さの比を求めるだけ。
愛光1枚目のサービス問題程度のレベル。
[3]条件整理
勝っても負けても点がもらえるじゃんけんの点数差を考える。
勝ち負けの手の組み合わせを条件整理するだけで解決、超易しい。
[4]場合の数
正三角形格子に正三角形が大小あわせて何個あるかを数える。
1辺が5マスだから、高知県の普通の上位生でも正解できる。
せめて格子じゃなく点に変えた上でスケールを増やすくらいでないと。
[5]数の性質/場合の数
「ABABA」の5ケタの整数で倍数条件を満たす個数を求める。
下2ケタだけを取り出し、Bは0でもOKであることに注意するだけ。
[6]規則性
規則に従って作成した整数が2で何回割り切れるかを求める。
一瞬身構えてしまうが、小さい数から規則を探っていけば簡単。
解いてみれば易しいけれども、なかなか興味深い規則だ。
[7]数の性質
4×4の積の魔方陣を作成する。
わかっている数をひとまず素因数分解することが解決の第一歩。
解が2つある点が少し意外で、一部受験生の手がここで初めて止まる?
[8]周期算
正三角形の紙を少しずつずらせて重ねていく問題。
H23高知学芸などでも類題のある、非常に典型的な問題である。
[9]相似
合同な2つの三角形を置いたとき、指定された長さを求める。
ようやく、発想が要求される灘らしい良問の登場である。
とはいえ、難しいと言うほどのものではないが。
ひょっとして、H21灘第2日[5](1)直角三角形6個置きが元ネタか?
少し雰囲気が似ているし、どちらも同じ方法で解けるようなので。
[10]面積比
二等辺三角形に何本か線を引いたときの面積や長さを求める。
どう見てもベンツ斬りです本当にありがとうございm(ry
関西圏では腐るほど演習するだろう題材の典型題で、間違える人は稀。
[11]平面図形/点の移動
円の内部にある線分の中点の軌跡について考察する。
中学~高校の直輸入問題で、相似縮小が身についていれば問題なし。
[12]立体図形/推理
投影図から、積み上げた立方体の個数を推理する問題。
これは完全に、高知県の入試レベルの典型題。
あえて注意点を挙げるなら、最小個数は1段だけの所があるくらい。
後半は体積でなく「表面積の最大値」くらいの試練があってもいいよ…。
[13]立体図形/展開図
2種類の展開図を組み立てたときの体積比を求める。
AもBも大きな正四面体に埋め込めることに気付けるかが勝負。
でも、この程度のことは灘中受験生は対策済だと思うんだけど。
★算数第2日
[1]濃度算
2つの食塩水を混ぜたときの重さや濃度変化についての問題。
具体的な重さの条件が何ら与えられていないが、落ちついて全体の重さや食塩水の重さの変化の条件から重さの比を求めればよい。
愛光松山会場平均層でもそこそこ完答が出そうなくらいのレベルであり、この程度の処理を灘受験生ができなくてどうする、って感じ。
[2]立体図形や平面図形の構成
立方体から切り出した立体の切断面を下にしたときの高さを求める。
有名な三角すいの変形版であるが、もちろんその有名バージョンと同じ解き方で解決できる。
まだ中学入試では殆ど出題されていないが、算チャレ等では10年以上前から何度か出題されている…算チャレは受験算数の10年先を行く?
(3)は辺の比が1:2と1:3の直角三角形の角度の和を求めるもので、中学入試を受けるなら誰もが知っているであろう超有名タイプ。
[3]ニュートン算
タンクの水量が少なくなると排水管の性能が変化するニュートン算。
設定がなんやかんやで複雑ではあるものの、閃きは特に必要ないため、条件を整理して手堅く解ききりたいところ。
[4]規則性
タイルで作った長方形に対角線を1本引いて通るタイルの数の問題。
確かS61に「対角線を2本引いたときに通過しないタイルの個数をもとに長方形の横を求める」問題があったと思うので、(1)はそれの劣化版か。
(2)はこれを立体版にしたもので少し骨があるものの、H3やH9に出題されたものの類題と言えるので、新顔の難問かといえばそうでもない。
[5]場合の数
格子状の道を行く兄から弟が見える進み方について考える。
どの進み方だと兄から弟が見えないのかを要領よく調べる必要があり、易しくはないが難しくもない。
設定はなかなか面白いが、弟の進み方がすべて指定されており、問題が尻切れ気味で終わっているのが残念。
かといって、兄と弟の進み方の組み合わせを全部求めようとすると、かなり面倒なことになってしまうようだが。
改めて今年の問題を眺めていると、特に第2日の小問の助長さが目立っている。。
★この一題
第1日と第2日から1つずつ選んでみよう。
・第1日[9]
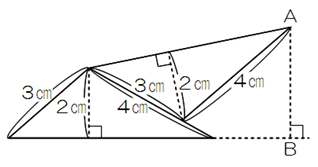
合同な三角形を上の図のように置いたとき、ABの長さは□cmです。
→解説つくりました
・第2日[4] ※図省略
(1)一辺の長さが1cmの正方形の形をしたタイルをすきまなく並べて長方形を作り、この長方形の一つの対角線に沿ってタイルを切ったとき、切られたタイルの個数を数えます。
1. タイル15個を縦5cm、横3cmの長方形に並べたとき、切られたタイルは何個ですか。
2. タイル5184個を縦81cm、横64cmの長方形に並べたとき、切られたタイルは何個ですか。
3. タイル11664個を縦144cm、横81cmの長方形に並べたとき、切られたタイルは何個ですか。
(2)一辺の長さが1cmの立方体の形をした透明なブロックを、すきまなく並べて直方体を作ります。この直方体の1つの頂点から、残り7つの頂点の中で最も遠い頂点に向かって光線を発射します。光線はまっすぐ進み、ブロックによって反射や屈折をしたり、方向が変化したりすることはありません。この光線が貫いているブロックの個数を数えます。ただし、光線がブロックの頂点のみを通っている場合や辺のみを通っている場合は、光線がブロックを貫いているとは考えません。
ブロック202500個を縦75cm、横90cm、高さ30cmの直方体に並べたとき、貫かれたブロックは何個ですか。
→解説つくりました
PR

