(1)これは定番中の定番。
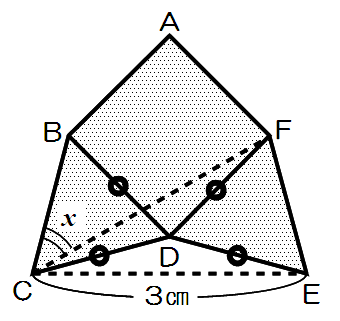
図のようにA~Fをふる。
CD=BD=DFより、△CDFは二等辺三角形。
角CDF=60+90=150度だから、角FCDは(180-150)÷2=15度。
よって角x=60-15=
45度…答
(2)これが難問。
角度計算をしているとき、△CDFと△CDEは合同であることに気付いただろうか?
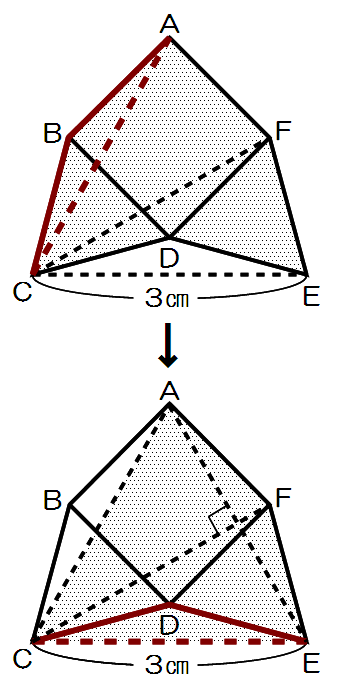
ACを結ぶと、△ABCもこれらの三角形と合同である。
そこで、△ABCの面積を△CDEの部分にはめこみ移動することができる。
すると、求める面積は、四角形ACEFである。
AC=CE、角ACE=60度より△ACEは正三角形で、角CAE=60度。
また、CE=CFでもあるので、AE=CF=CE=3cmである。
そして(1)より、角ACF=45-15=30度なので、AEとCFは直角に交わることがわかる。
対角線が直角に交わる四角形の面積は「対角線×対角線÷2」で求められる。
よって面積は3×3÷2=
4.5cm2…答
原題ではくどいくらいのヒントがあって、せっかくの良問がただの簡単な問題になってしまっているが、ここでは省いた。
PR

