AとBが1回目にすれ違う地点をX、2回目にすれ違う地点をYとしてダイヤグラムを描く。
(時間の計算…8:36-8:00=36分 9:24-8:36=48分)
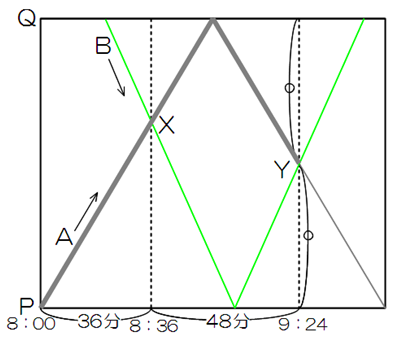
(1) Y地点がPQ間の真ん中であることに注意すると、AがPを出発してからQを折り返してYに達するまでに進んだ道のりは
片道1.5個ぶんであり、それだけ進むのに36+48=
84分かかっている。
AがPQ間、つまり片道1個ぶん進むのにかかる時間は、84÷1.5=56分。 …(☆)
よってAが一往復するのにかかる時間は56×2=112分だから、答えは8時0分の112分後で
9時52分。
(2) ☆より、AがXQ間を進むのに56-36=20分かかる。PX間とXQ間の距離の比は、Aが進むのにかかる時間の比に等しく36:20={9}:{5}である。
するとPQ間の距離は{9}+{5}={14}なので、QY間およびYP間の距離はともに{14}÷2={7}である。
1回目のすれ違いから2回目のすれ違いまでの48分間に、Aは{5}+{7}={12}、Bは{9}+{7}={16}だけ進んでいる。
AとBの速さの比は48分間に進んだ道のりの比に等しく、{12}:{16}=
3:4である。
(3) AとBがQX間を進むのにかかる時間は速さの逆比で4:3だから、BがQX間を進むのにかかる時間は20÷4×3=15分である。よって、BがQを出発したのは8時36分の15分前で、
8時21分。
(1)の太字部分から話を膨らませることができなければ、どうにもならない怖い問題だ。
PR

